聚类

简单记录一下聚类。

无监督学习：训练集没有标签，聚类就是一个典型的无监督学习应用。

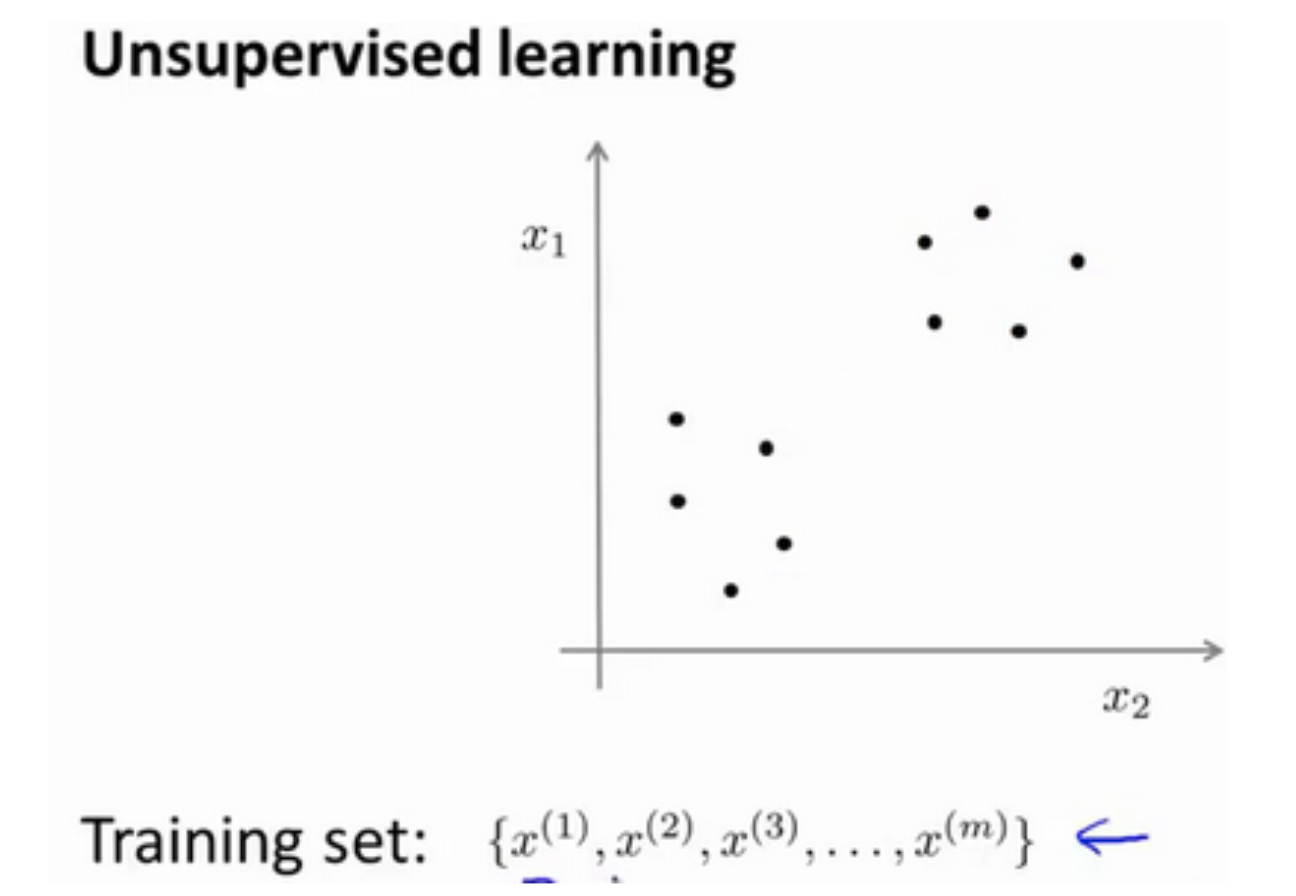
聚类算法可以把上图分类两个簇。

K-Means 算法

K-Means 是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

例如我们想将数据分成 k 个分组，k-means 算法首先选择 k 个随机点，这 k 个随机点称为 聚类中心（cluster centroids）

每一个聚类中心相当于“分组”的中心，k-means 算法优化目标是最小化所有数据与聚类中心点距离的距离和。

K-means 算法是一个迭代算法，每一次迭代完成两件事情

• 计算每个数据最近的聚类中心，即为聚类中心关联数据（优化目标1）
• 用聚类中心关联的数据点平均分布位置更新该聚类中心 （优化目标2）

k-means 算法优化目标

优化目标(1)

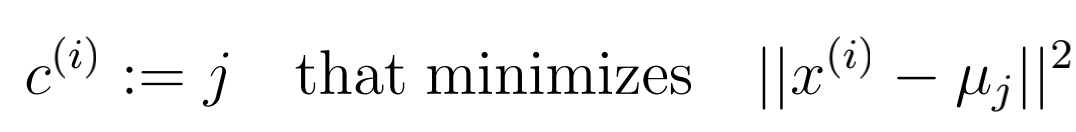
$c^{(i)}$ 是第 i 个样本 $x^{(i)}$ 最近的聚类中心的下标, $\mu_j$ 是第 j 个聚类中心的向量。

优化目标(1) 的目标是找一个 j 使得 $x^{(i)}$ 到该聚类中心 $\mu_j$ 的距离最短（换句话讲，就是找到离 $x^{(i)}$ 最近的聚类中心, 并将该聚类中心的下标对应的下标赋值给 $c^{(i)}$）

通俗点讲，为聚类中心关联数据向量

优化目标(1)的代码实现

function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
%   idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
%   in idx for a dataset X where each row is a single example. idx = m x 1 
%   vector of centroid assignments (i.e. each entry in range [1..K])
%

% Set K
K = size(centroids, 1);

% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);
for i = 1:size(X, 1)
    a = zeros(size(centroids));
    for j = 1:size(centroids, 1)
        a(j, :) = X(i, :);
    end
    distance = sum((a - centroids).^2, 2);
    [~, idx(i)] = min(distance);
end

% =============================================================
end

优化目标(2)

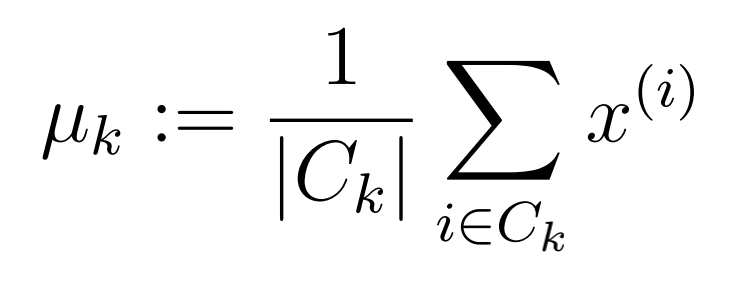
优化目标(2) 的作用是优化聚类中心。 $\mu_k$ 表示聚类中心，$C_k$ 是一个集合，用来记录聚类中心 k 对应的关联数据的集合，$|C_k|$ 是集合中元素的个数。

优化目标(2) 的代码实现

function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returns the new centroids by computing the means of the 
%data points assigned to each centroid.
%   centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by 
%   computing the means of the data points assigned to each centroid. It is
%   given a dataset X where each row is a single data point, a vector
%   idx of centroid assignments (i.e. each entry in range [1..K]) for each
%   example, and K, the number of centroids. You should return a matrix
%   centroids, where each row of centroids is the mean of the data points
%   assigned to it.
%

% Useful variables
[m n] = size(X);

% You need to return the following variables correctly.
centroids = zeros(K, n);

sums = zeros(K, n);
sums_counter = zeros(size(idx, 1), 1);

for j = 1 : size(idx, 1)
    sums(idx(j), :) = sums(idx(j), :) + X(j, :);
    sums_counter(idx(j)) = sums_counter(idx(j)) + 1;
end

for i = 1 : size(sums, 1)
    sums(i, :) = sums(i, :) ./ sums_counter(i);
end

centroids = sums;

% =============================================================
end

随机初始化聚类中心

k-means 结果对于初始的聚类中心选择非常敏感，在运行 k-means 算法之前，我们应该选择随机的聚类中心。一般随机选择 k 个数据点作为聚类中心。多次用随机初始化的聚类中心运行 k-means 算法，选择误差最小的为最优模型。这样可以避免迭代算法达到局部最优解。