Ml3:Classification
Classification
模型
分类问题中,预测的变量 y 为离散值,以前学习的线性回归模型就不适用了。分类将用到的算法是逻辑回归( Logistic Regression )。
我们先讨论二元的分类算法,即把输入分成两类,也就是说 y 的值为 0 或 1.
逻辑回归假设函数:$h_\theta(x)=g(\theta^Tx)$ 该函数值的范围始终是 0 到 1 之间。
当 $h_\theta(x) >= 0.5$ 时,预测 y = 1
当 $h_\theta(x) < 0.5$ 时,预测 y = 1
可以理解为 $h_\theta(x)$ 是计算给定输入,输出为 y=1 的可能性。
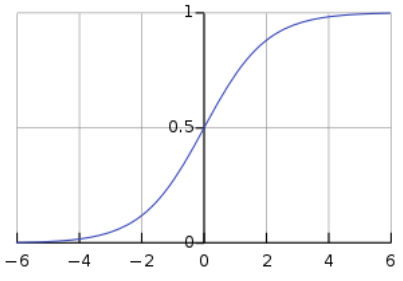
其中 g 代表的是逻辑函数,课程中选的逻辑函数叫 Sigmoid function, 该函数的图形是 S 形。
$g(x) = \frac{1}{1+e^{-x}}$
决策边界
简单说,就是假设函数所确定的图形线。这个例子中我们有:
当 $h_\theta(x) = g(\theta^Tx) >= 0.5$ 时,预测 y = 1
当 $h_\theta(x) = g(\theta^Tx) < 0.5$ 时,预测 y = 1
根据 Sigmoid 函数性质,可以继续得出:
$\theta^Tx >= 0$ 时,预测 y = 1
$\theta^Tx < 0$ 时, 预测 y = 0
在图中画出 $y = \theta^Tx$ 的图形,如图
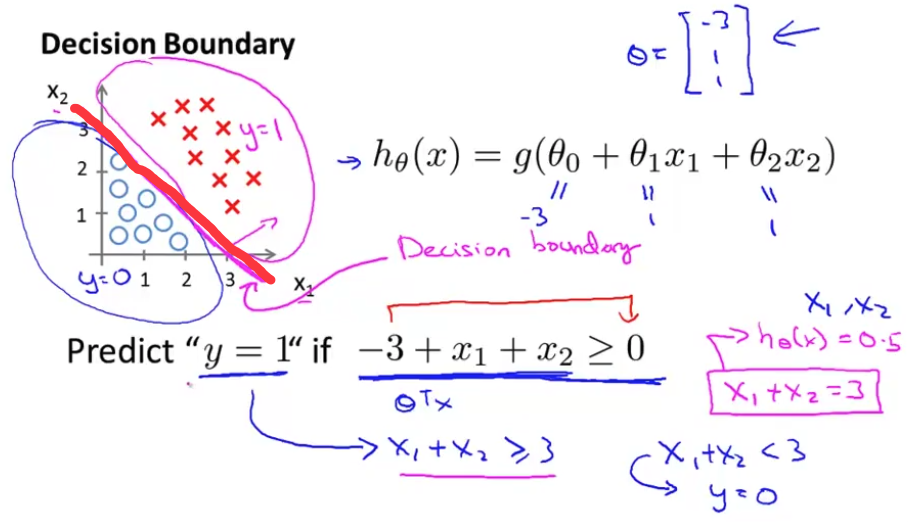
红色的线就是决策边界,将样本分为两类。所谓决策边界就是能够把样本正确分类的一条边界,主要有线性决策边界(linear decision boundaries)和非线性决策边界(non-linear decision boundaries)。注意:决策边界是假设函数的属性,由参数决定,而不是由数据集的特征决定。
非线性的决策边界

代价函数
逻辑回归假设函数的代价函数如何来选择呢?如果将 $h_\theta(x)=g(\theta^Tx)$直接带入线性回归的代价函数的话,代价函数存在局部最优解,将得到一个非凸函数(non-convexfunction)。这种非凸函数会干扰梯度下降算法,使梯度下降算法在某个局部最优解收敛。
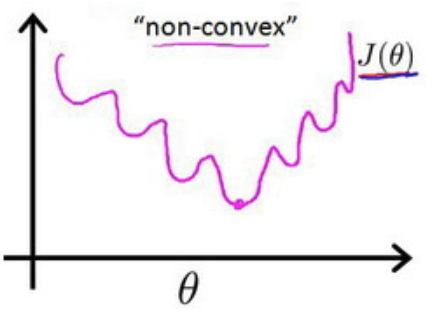
如何设计代价函数来避免这种情况呢?
重新定义代价函数 $J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}Cost(h_\theta(x^{(i)}),y^{(i)})$,cost的定义如下
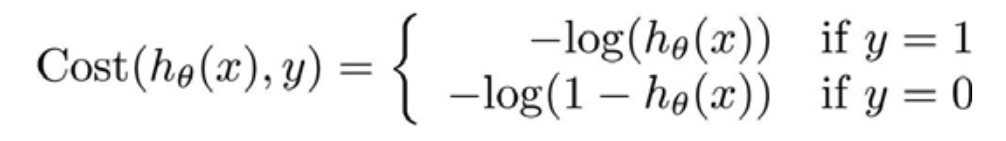
这个 Cost 可以进一步化简合并一下,很简单,就不写出来了。$h_\theta(x)$ 与 Cost 函数的图像如下。
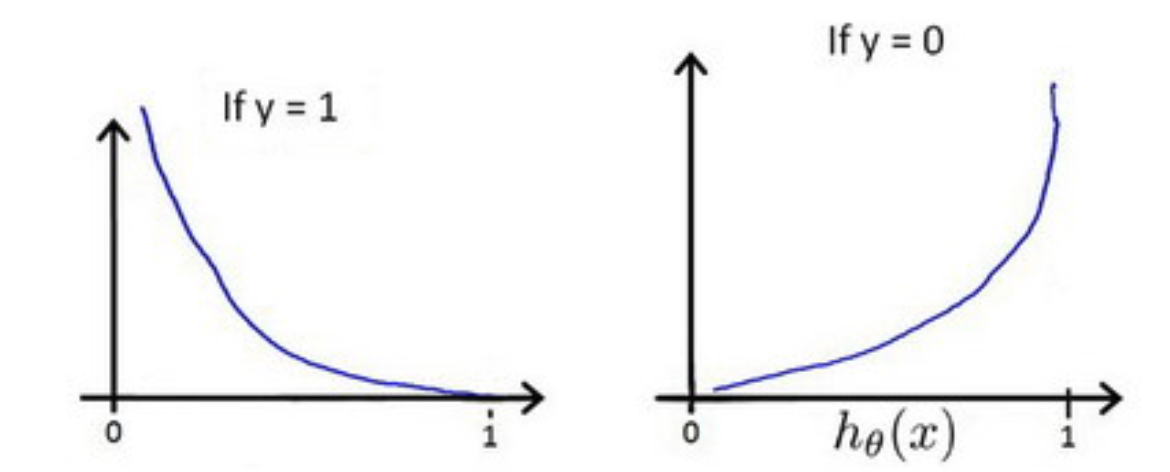
假如训练集中某样本 y = 1,$h_\theta(x)$ 要趋于1 的时候误差才最小,反之亦然。
这样,定义代价函数后,就可以使用梯度下降算法求最优参数解。
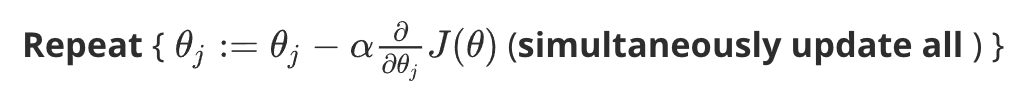
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!