Linear Regression

寒假无聊，就打算学习机器学习。

课程地址: https://www.bilibili.com/video/BV164411b7dx?p=1

学习机器学习的过程中，第一个要学的算法就是线性回归。通过学习线性回归算法，可以了解到机器学习中的监督学习(Supervised Learning) 基本流程。高中数学课程已经讲过线性回归，但是仅仅是给出了计算公式，其中的原理从没有讲过。

单变量线性回归(Linear Regression with One Variable)

模型表示

课程以预测房子价格为例子，目的是使用给定的数据集训练模型，使该模型能够预测房子价格。该例子只有一个变量即房子的面积。

训练集如下图：

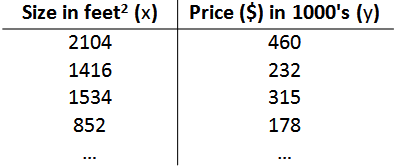
面积与价格之间存在某种线性关系，如下图

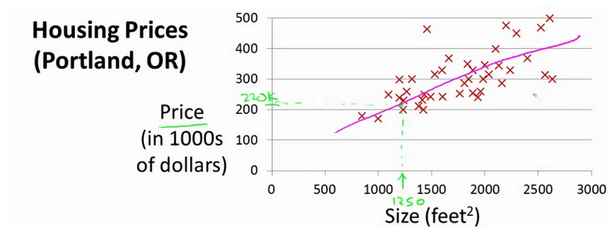
我们把这种线性关系假设为一个hypothesis 即 $h_\theta(x) = \theta_0 + \theta_1x$

模型如下图：

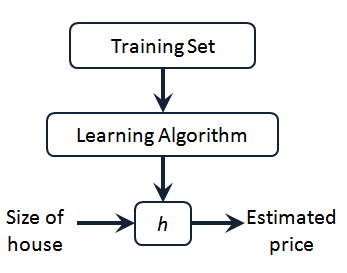
h 代表的是 hypothesis ，即 $h_\theta(x) = \theta_0 + \theta_1x$ 。 Learning Algorithm 的作用是用 Training Set 中的数据求出满足要求的 $\theta_0$ 和 $\theta_1$

一些符号定义

$m$ 代表训练集中实例的数量

$x$ 代表特征/输入变量

$y$ 代表目标变量/输出变量

$(x,y)$ 代表训练集中的实例

$(x^{(i)},y^{(i)})$ 代表第 $i$ 个观察实例

代价函数 cost function

如何选择 $h_\theta(x) = \theta_0 + \theta_1x$ 中的 $\theta_0$ 和 $\theta_1$ 参数，使得 h 可以很好的预测呢？

这时候就引入 cost function 来表示假设函数与真实数据（训练集中的数据）之间的差异。训练的目的就找到合适的参数，使代价函数的值最小化。

这个例子中代价函数定义 : $J(\theta_1,\theta_2) = \frac{1}{2m}\sum\limits_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})^2}$

代价函数的图像

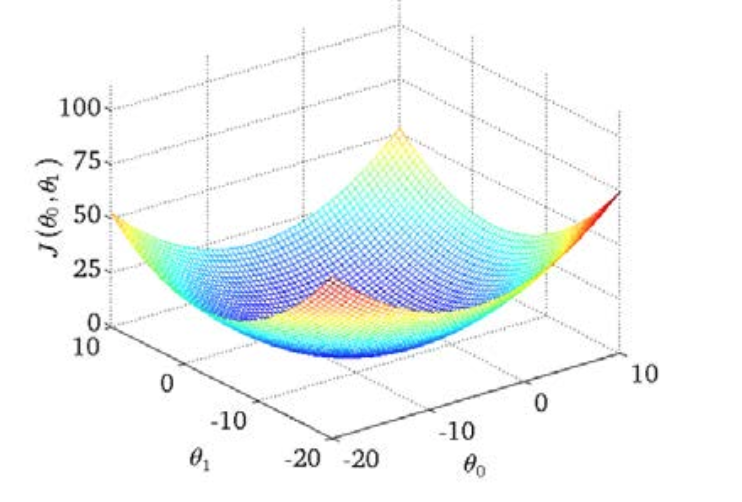
通过该图，可以找到一个代价函数的最小点对应的参数值。训练的目的就是找到代价函数最小值对应的参数，这样假设函数计算值与训练集之间的差异就很小。

梯度下降法 (Gradient Descent) 最小化代价函数

类似爬山一样，我可能在山上的任意一个位置，我要如何走才能到山底呢？

梯度下降法就是一种最小化代价函数的算法，梯度下降背后的思想是：开始时我们随机选择一个参数的组合 $(\theta_1,\theta_2,……,\theta_n)$，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

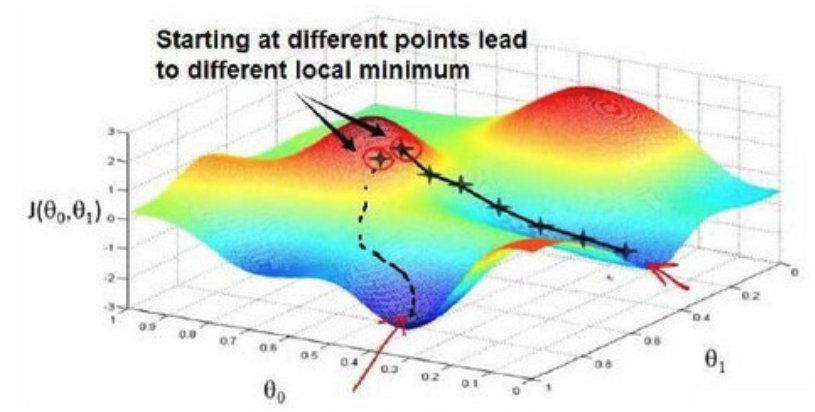
用数学语言表达下降的一步就是

$\theta_0 := \theta_0 - \alpha\frac{\delta}{\delta\theta_0}J(\theta_0,\theta_1)$

$\theta_1 := \theta_1 - \alpha\frac{d}{d\theta_1}J(\theta_0,\theta_1)$

其中 $\alpha$ 是学习率，如果学习率太小，下降的速度就太慢了，如果学习率过大，可能就错过最小值。

每一步下降，参数值减去学习率乘代价函数的导数。

为了进一步理解下降的过程，考虑代价函数只有一个参数，代价函数的图像类似一个二次函数

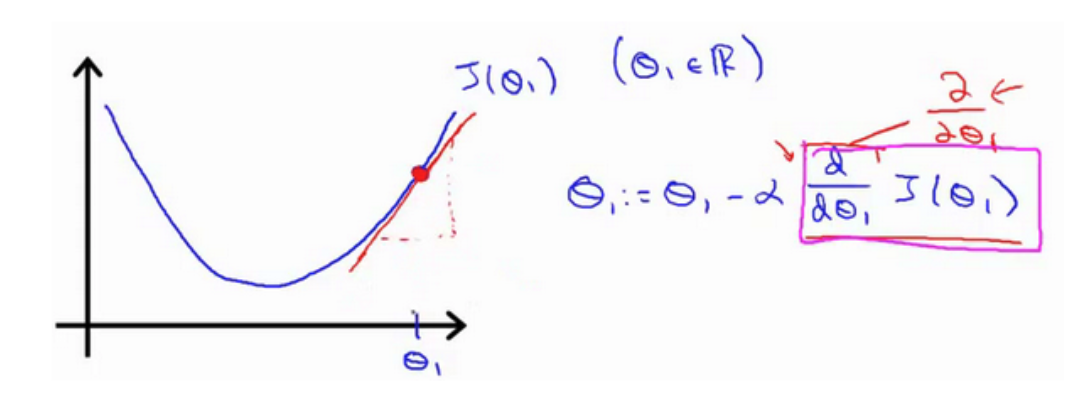
如图点 $\theta_1$ 对应函数值点处的导数，是一个正导数，即 $h’(\theta_1) > 0$，为了达到局部最小值，需要向左移动。 因此 $\theta_1$ 应该减去一个正数乘以 $\alpha$。导数项的作用之一就是确定 $\theta_1$ 更新的方向。通过多次迭代更新 $\theta$ 的过程，一直到收敛。

$\alpha$ 是学习率，作为导数项的系数，控制下降的步伐，如果太小，则迭代次数增加，如果太大，则可能直接错过最优解，甚至无法收敛。

迭代过程中，越接近 J 的最小值，导数项的值越小，即收敛。

该例子中的梯度下降完整描述

注意 $\theta$ 参数的更新是同时进行，如下图

线性回归中的梯度下降

主要是要求出代价函数的导数，多个变量求导，就是偏导数

偏导数学习：

https://www.bilibili.com/video/BV1sW411775X?from=search&seid=5642399025096029476

https://blog.csdn.net/qq_40241957/article/details/102659982

$\frac{d}{\delta\theta_j}J(\theta_0,\theta_1) = \frac{\delta}{\delta\theta_j}\frac{1}{2m}\sum\limits_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})^2}$

当 j = 0 时: $\frac{\delta}{\delta\theta_0}J(\theta_0,\theta_1) = \frac{1}{m}\sum\limits_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}$

当 j = 1 时: $\frac{\delta}{\delta\theta_1}J(\theta_0,\theta_1) = \frac{1}{m}\sum\limits_{i=1}^{m}{((h_\theta(x^{(i)})-y^{(i)})·x^{(i)})}$

重复上述过程得到批量梯度下降算法。

正规方程(normal equation)求代价函数最小

留个坑，目前还看不懂正规方程的推导过程。

$\theta = (X^TX)^{-1}X^Ty$

涉及到矩阵乘法，维数大了之后运算会很慢。

多变量线性回归

我们探讨了单变量/特征的回归模型，现在我们对房价模型增加更多的特征，例如房间数楼层等，构成一个含有多个变量的模型，模型中的特征为 $(x_1,x_2,……,x_n)$

如图训练集构成一个特征矩阵。

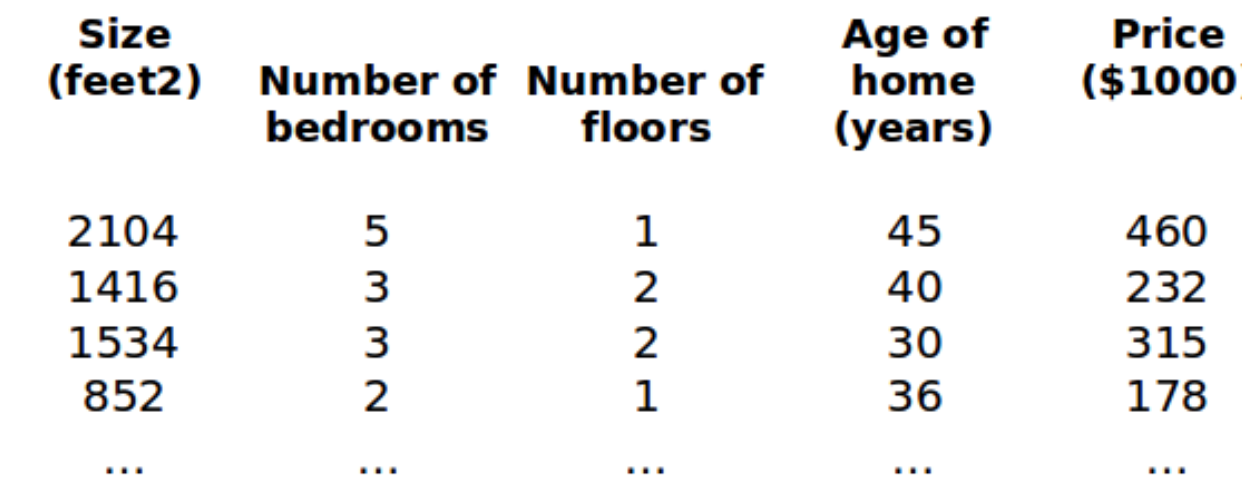
$n$ 代表特征数量

$x^{(i)}$ 代表第 i 个训练实例，是特征矩阵的第 i 行，是一个列向量

$x^{(i)}_j$ 代表第 i 行，第 j 个特征

多变量的假设函数: $h_\theta(x) = \theta_0x_0+\theta_1x_1+…+\theta_nx_n = \theta^TX$

其中令 $x_0 = 1$

多变量梯度下降

代价函数 $J(\theta1,\theta2,……,\theta_n)=\frac{1}{2m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})$

假设函数 $h_\theta(x)=\theta^TX$

梯度下降算法为:

Repeat {

$\theta_j := \theta_j - \alpha\frac{\delta}{\delta\theta_j}J(\theta_1, \theta_2,……,\theta_n)$

}

求导后为:

Repeat {

$\theta_j := \theta_j - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}((h_\theta(x^{(i)})-y^{(i)})·x^{(i)}_j)$

}

Repeat 的意思是循环直到收敛，注意赋值是同时进行。

over…. 打 latex 太累了。

梯度下降: 特征缩放

就是把特征数据缩放到较小的区间，例如 $[-3, 3]$ 有利于减少迭代次数，更快收敛

最简单的方法是令 $x_n=\frac{x_n-\mu_n}{s_n}$ 其中 $\mu_n$ 是平均值，$s_n$ 是标准差

多项式回归

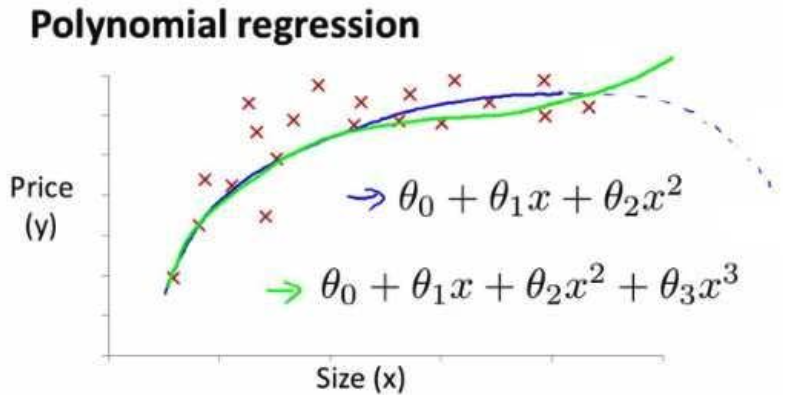
我们可以令

$x_1=x^0$

$x_2=x^1$

$x_3=x^2$

$x_4=x^3$

将该模型转化成线性回归模型。

根据图像的性质，我们可以使

$h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2$

或者

$h_\theta(x)=\theta_0+\theta_1x+\theta_2\sqrt{x}$

注：如果我们采用多项式回归模型，在运行梯度下降算法前，特征缩放非常有必要。

最后，还是一个不会写代码的咸鱼，准备这几天找到数据试试。