Context-Free Grammars

Brief Introduction

正则文法 VS 上下文无关文法

正则文法不能表示程序语言的递归结构，递归结构在程序语言中非常常见，比如 if 中可以嵌套 if、括号中可以嵌套括号、表达式中可以嵌套表达式。

正则文法无法识别 ((())) 这种具有递归形式的结构，因为正则文法不具备动态记忆功能，即没有一个正则表达式能识别 n 个 ( ，后再识别 n 个 )。

正则表达式 (*)* 可以成功匹配:
()
(())

(((()

如果用正则表达式，最后一组可以匹配成功，显然最后一组语法上是错误的。

Context-Free Grammars (CFG) 则可以很好的解决递归问题, CFG 中识别递归括号可以这样表示

S -> '(' S ')'
S -> ε

上下文无关文法中，这里的 S 可以称为 非终结符(non-terminal) ，非终结符可以进行进一步的推导，直到不存在非终结符。推导的过程就是将左部(LHS)替换成右部(RHS)。

‘(‘ 、 ‘)’ 称为终结符。

推导(Derivation)

推导 ： (())

r1: S -> '(' S ')'
r2: S -> ε

从开始符 S 开始推导
用规则 r1 替换 S     得到（S）
用规则 r1 替换 (S)   得到 ((S))
用规则 r2 替换 ((S)) 得到 (()) 
(())  不存在非终结符，推导完成。

推导可以画成语法解析树（Parse Tree）

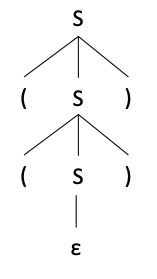
推导方式

最左推导:
每次替换最左侧第一个非终结符

最右推导:
每次替换最右侧第一个非终结符

如果一个 CFG 存在歧义(Ambiguous)，最左推导和最右推导将得出不同的 Parse Tree。

Backus Naur form (BNF)

普通记法

E -> E * E
E -> E + E

Backus Naur

E: E * E | E + E

Yacc 里面采用 BNF 范式

Ambiguous

例如用如下 CFG 定义四则运算

E -> E + E
E -> E * E
E -> ( E )
E -> -E
E -> id

推导 id + id / id

可以推导出两种 Parse Tree

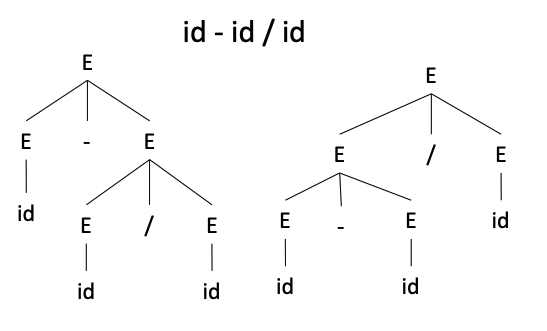
如何解决歧义？

1. 重新设计文法，使文法没有歧义
2. 指定优先级 (yacc 里面用 %left、%right，具体参考 blog 文章 Yacc practice )
3. 规定一些语法结构消除歧义

1，2 主要是利用优先级和结合性消除歧义。

如何设计优先级消除歧义？

这是一个有歧义的文法

E -> E - E
E -> E / E
E -> ( E )
E -> id

推导 id - id / id 存在歧义。

引入另外一个非终结符，使文法推导 id - id / id 没有歧义

E -> E - E      E -> T
T -> T / T      T -> F
F -> id         F -> (E)

无论采用最左推导还是最右推导，只能得到一颗 Parse Tree

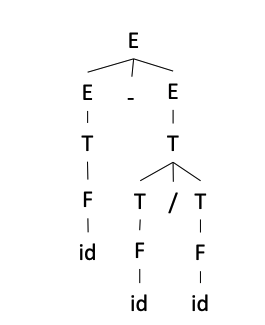
如何利用结合性消除歧义？

引入 T 后消除了 id - id / id 的歧义，但是推导 id - id - id 仍然存在歧义，如图：

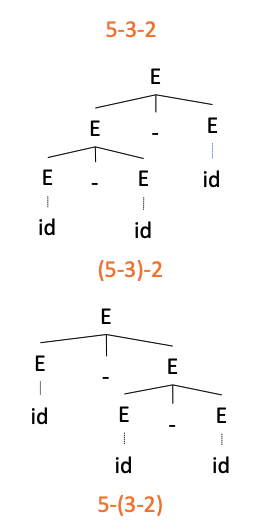
‘-‘ 运算符采用左结合，所以改写为左递归文法

E -> E - E
E -> E / E
E -> ( E )
E -> id

改写为

E -> E - T      E -> T
T -> T / F      T -> F
F -> id         F -> ( E )

YACC 中消除歧义

参考这篇 Yacc practice 中的 实现优先级和结合性

Pushdown automata, PDA

下推自动机

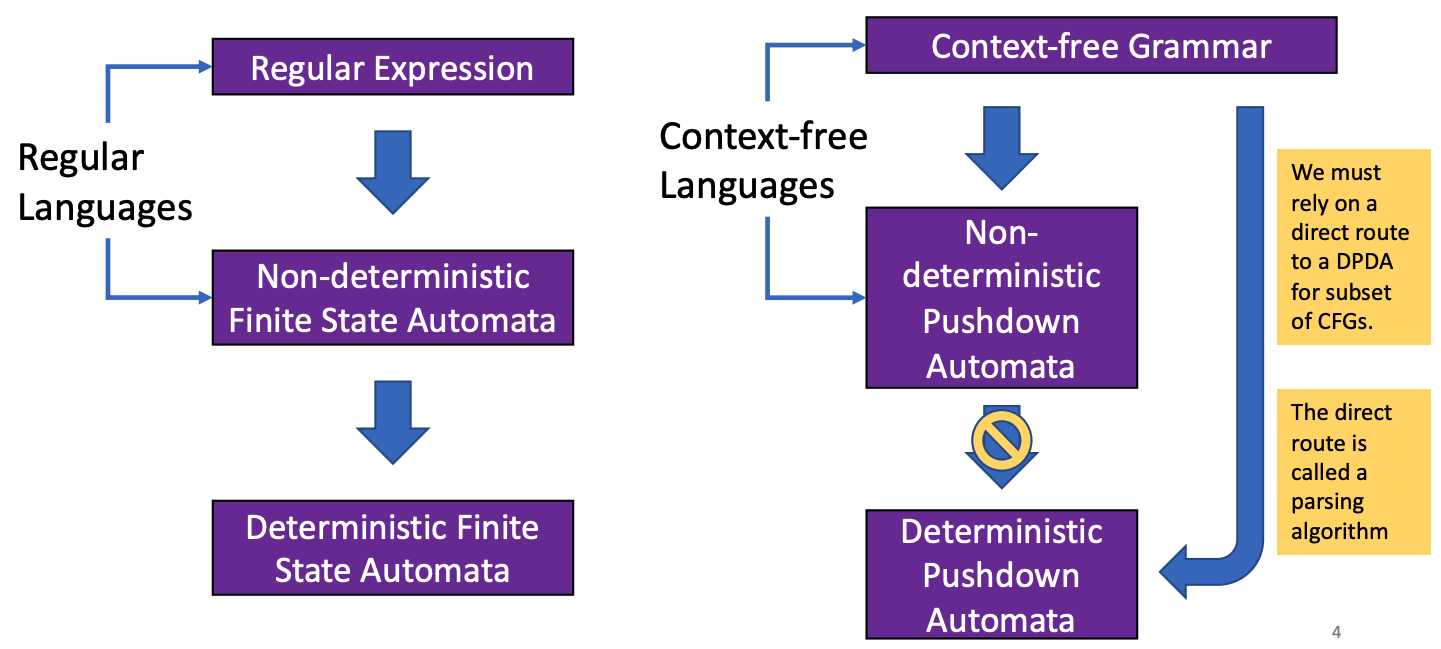
正则表达式有一个对应的有限状态自动机，上下文无关文法也有一个对应的下推自动机。pushdown automata 其实就是一个栈 + FSA。

下推自动机 vs 有限状态自动机

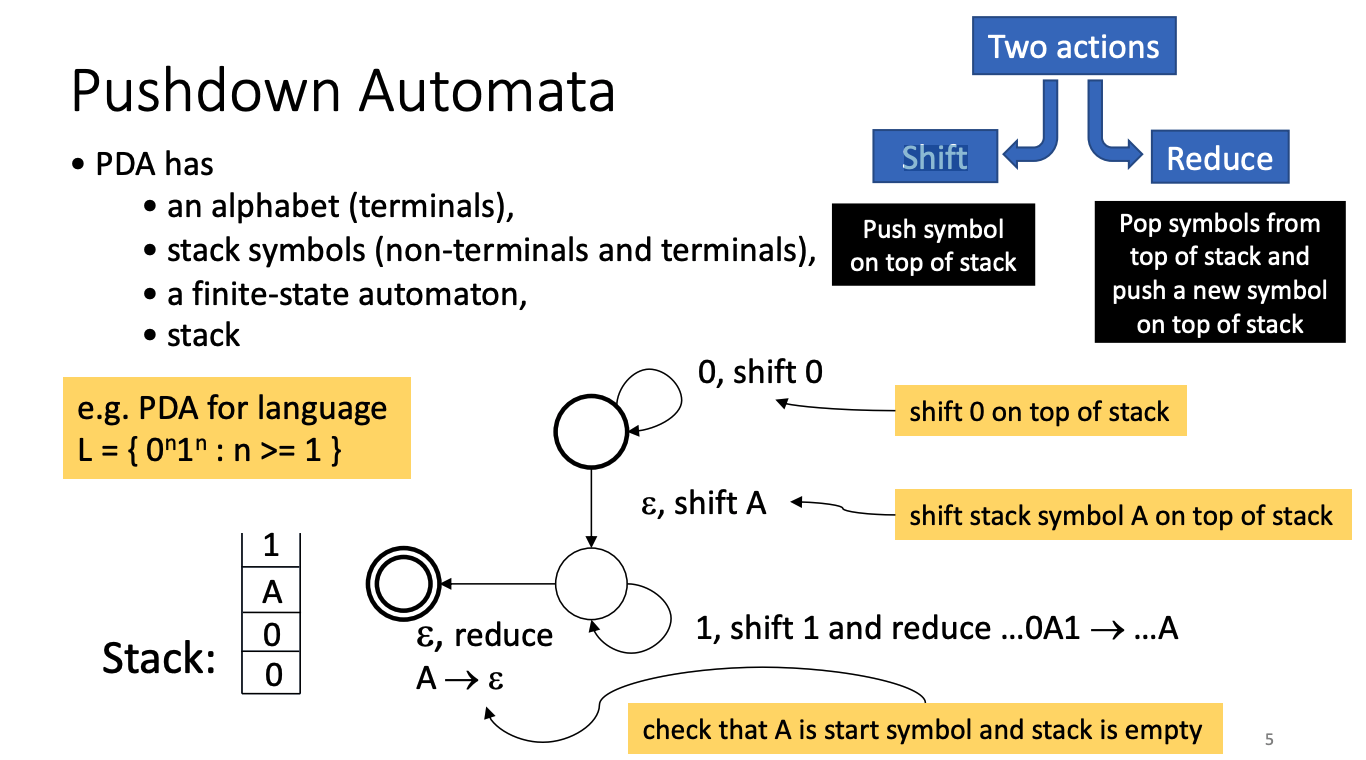
下推自动机的两种操作

• Shift 入栈
• Reduce 出栈根据合并再入栈

简单讲，就是将遇到的符号入栈，如果栈顶的某几个元素满足某条规则，则用该规则对这几个元素进行 Reduce。